Bei Osiander in Überlingen fand ich per Zufall das Buch von
Malcolm Hislop:
„Wie baut man eine Kathedrale“.
Ich stieß unter anderem auf ein interessantes Kapitel über geometrische Regeln, die von den Baumeistern der großen gotischen Kathedralen – hier vorwiegend französische und englische Kathedralen – angewendet wurden. Hier las ich:
Die Geometrie ist das Herz der Entwürfe mittelalterlicher Kathedralen, denn die Proportionen von Entwürfen, Profilen und Fassaden wurden aus geometrischen Figuren abgeleitet. Sogar Details wie Kreuzblumen, Fenstermauerwerk und Zierleisten basieren auf geometrischen Figuren und wurden mit Zirkel und Winkelmaß gezeichnet.
Der Gesamtentwurf einer Kirche beruhte also auf der Geometrie mit ihren Regeln der Proportionalität. Am bekanntesten war die Gleichung 1: √2 (1:1,41), die das Verhältnis der Seite eines Quadrats zu seiner Diagonale darstellt und daher leicht zu behalten und zu konstruieren war.
Und davon möchte ich hier berichten.
Was besagen die Regeln „ad quadratum“ und „ad triangulum“, wie lassen sie sich darstellen und wurden sie auch beim Bau des Überlinger St. Nikolaus Münsters angewandt?
zunächst die Regel „ad quadratum“. Sie besagt:
Das Verhältnis der Seite eines Quadrats zu seiner Diagonale wird als besonders harmonisch empfunden.
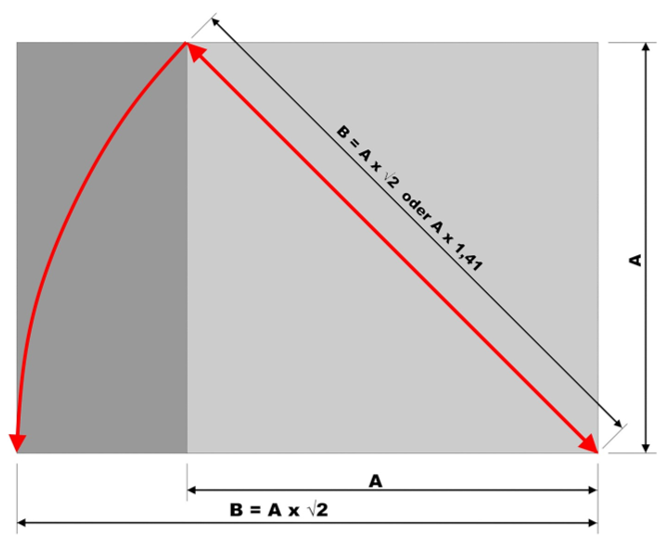
Diese Zeichnung zeigt ein Rechteck, das gebildet wird aus der Seitenlänge A eines Quadrats und der Diagonalen B. Das Seitenverhältnis A/B beträgt 1/√2. Eine mathematische Formel 1 / √2 ist auf einer Baustelle sicherlich unbrauchbar aber ein Rechteck in diesem Maßverhältnis ist mit einer Messleine sehr einfach zu konstruieren.
A. die Raumproportionen im Mittel- und Seitenschiff des Münsters
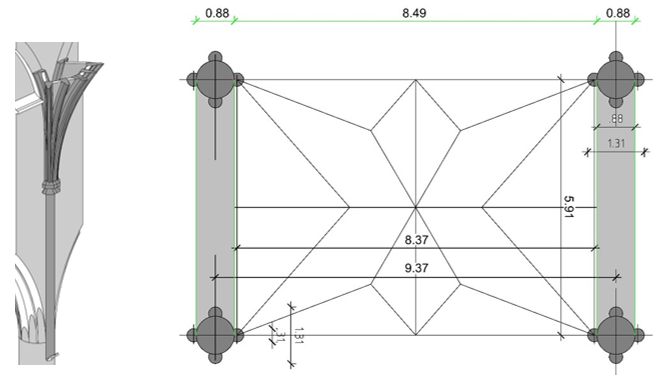
Dies ist der Grundriss eines Gewölbejochs des Mittelschiffs im Überlinger Münster mit den Messdaten aus einem Aufmaß während der Sanierung 1908-1924. Links die Darstellung eines Gewölbeanfängers über einem Dienst und Kapitell.
Wenn man in dieses Joch ein Rechteck nach den Regeln des „ad quadratum“ einzeichnet, erkennt man, dass nicht die Stützenachsen den Regeln des „ad quadratum“ unterliegen, sondern die Konstruktionspunkte der Gewölbeauflager, die Mittelpunkte der Dienste. Sie bilden ein Rechteck von der Größe 5,91m x 8,37m und nach der Regel „ad quadratum“ 5,91m x 8,358m, also mit minimaler Differenz von 1,2cm.
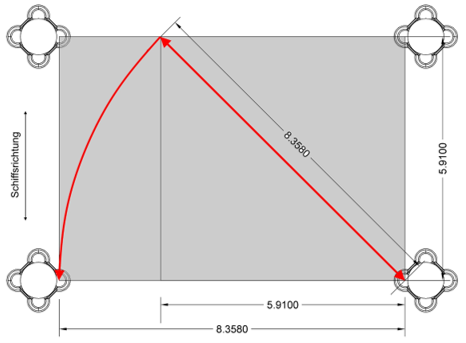
Bei dem Entwurf des Grundrisses wurde offenbar die Regel des „ad quadratum“ angewandt. Galt dies aber auch für die Ermittlung der Höhenmaße im Aufriss von Mittel- und Seitenschiff? Ich habe dies zunächst an folgendem 3D-Modell untersucht.
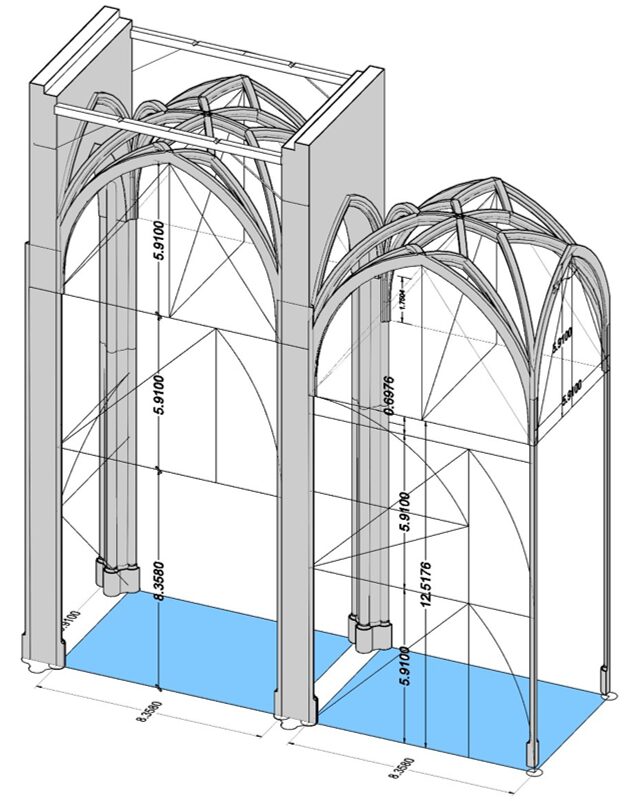
Auf den ersten Blick erscheint es denkbar, dass im Mittelschiff die Regel „ad quadratum“ angewendet wurde, kaum aber im Seitenschiff. War denn eine so komplizierte Ausführung auf einer mittelalterlichen Baustelle überhaupt möglich?
Daher meine Überlegung, ob eine konventionelle Messmethode nicht viel einfacher wäre? Die großen Raumproportionen zwar analog „ad quadratum“, die Vermaßung im Detail aber mit der Knotenleine in Ellen oder Fuß?
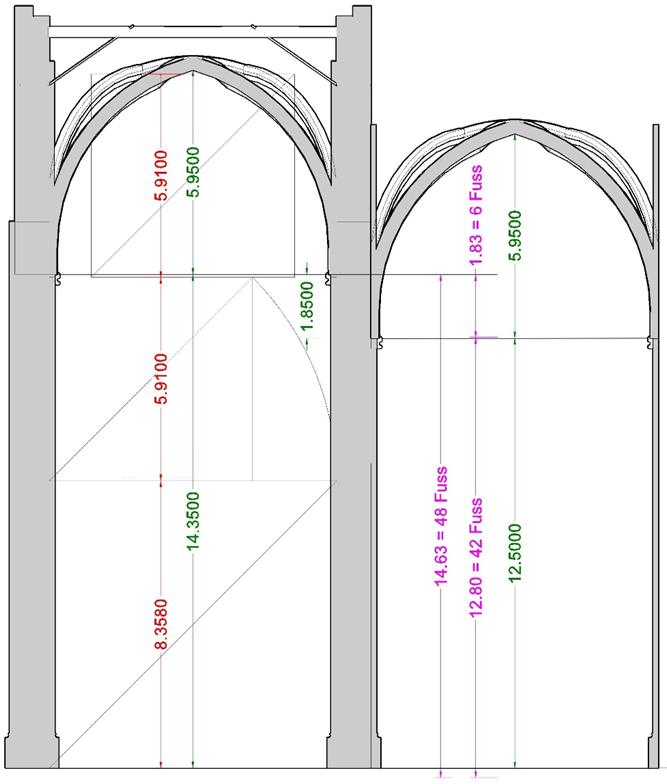
In oben stehendem Schnitt habe ichsind verschiedene Messmethoden eingezeichnet.
rot: gem. „ad quadratum“ eine Addition der Seitenmaße des Gewölbejochs 8,358m + 5,91m = 14,268m als Mittelschiff-höhe bis zum Kapitell und zusätzlich 5,91m bis zum Gewölbescheitel
grün: gem der Aufmaßblätter 53 und 62 ergibt sich ein Seiten-maß des Gewölbejochs von 14,35m bis zum Kapitell und 5,95m bis zum Gewölbescheitel im Mittelschiff
im Seitenschiff beträgt die Höhe bis zum Kapitell 12,50m und aus den Gewölberesten ist rekonstruierbar, dass ein gleiches Gewölbe wie im Mittelschiff geplant war, also ebenfalls mit einer Scheitelhöhe von 5,95m
die Differenz zwischen den Kapitellen im Mittel- und Seitenschiff beträgt 1,85m
Nach den Baubeschreibungen soll der Kirchenboden ursprüng-lich tiefer gelegen haben. Ein Maß habe ich leider nicht gefunden. Die Maße nach „ad quadratum“ und auch in den Aufmaßblättern beziehen sich aber alle auf die heutige Höhe des Kirchenschiffs.
Das einzige Höhenmaß, das mit Sicherheit der ursprünglichen Planung entspricht, ist die Differenz von 1,85m zwischen den Kapitellen, auch wenn das einzige erhaltene Kapitell im nördl. Seitenschiff leicht beschädigt und im heute darunter liegenden Gewölbekessel nur schwer einzumessen ist.
magenta: ein Versuch, eine einfache, handwerksgerechte Messmethode zu finden
Unter der Annahme, dass auf einer Baustelle normalerweise mit einer Knotenleine gearbeitet wurde mit einer Einteilung in Fuß, würde die Höhendifferenz der Kapitelle 6 Fuß = 1,83m betragen. Das Kapitell im Mittelschiff würde dann 48 Fuß und das des Seitenschiffs 42 Fuß (14,63m bzw. 12,80m) über dem ursprüng-lichen Boden liegen. Der ursprüngliche Boden läge also im Vergleich zum Aufmaß 0,28m unter dem heutigen Boden der Kirchenschiffe.
Nach einer erneuten Planänderung sollten die Seitenschiffe in gleicher Grundrissgröße aber mit niedrigeren, flacheren Gewölben ausgeführt werden. In den nördlichen Jochen 7 und 8 sind Bauteile dieser Planungs- und Bauphase erhalten.
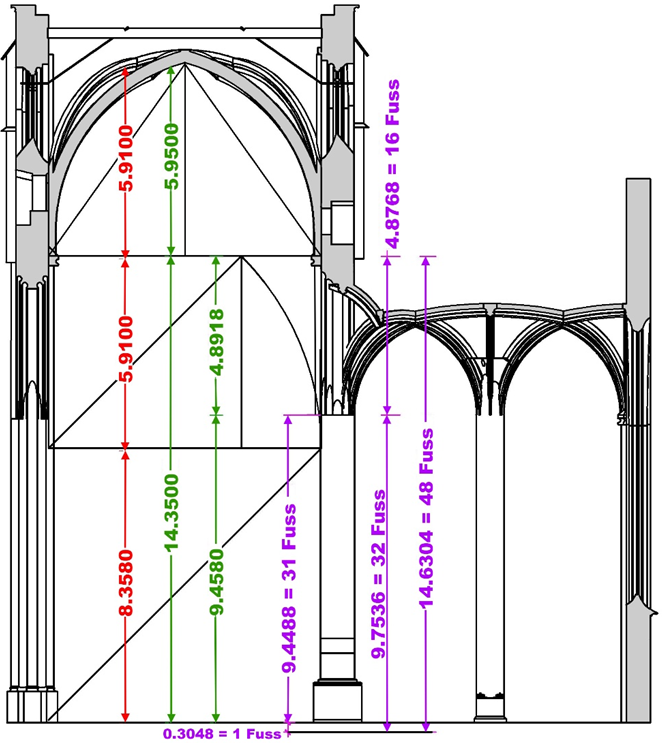
In diesem Schnitt sind:
rot: Maße gem. Regel „ad quadratum“
grün: Maße lt. Aufmaß Plan Nr. 53 und 62
magenta: Maße in Fuß
Gestalterische und konstruktive Merkmale lassen vermuten, dass diese Planänderung vom gleichen Baumeister ausgeführt wurde; dann sicherlich mit gleichen Bemaßungsmethoden.
In der nebenstehenden Schnittzeichnung beträgt die Höhe des niedrigen Seitenschiff-Kapitells lt. Aufmaß = 9,458m, mit Knotenleine wären 31 Fuß = 9,4488m. Das ist eine Differenz von nur 0,92cm
Der Höhenunterschied der Kapitelle beider Schiffe ist lt. Aufmaß = 4,8918m, mit der Knotenleine ergeben 16 Fuß = 4,8768m. Die Differenz zwischen Aufmaß und Berechnung in Fuß nur 0,15cm.
Diese unbedeutenden Maßdifferenzen legen nahe, dass auf der Baustelle die Höhen-maße nicht nach der komplizierten Methode „ad quadratum“ festgelegt wurden, sondern alle Höhenangaben in Fuß bemessen wurden.
Auffallend ist, dass die gemessene Höhe des Gewölbes im Mittelschiff zwischen Kapitell und Gewölbescheitel mit 5,95m dem Jochmaß nach „ad quadratum“ mit 10 Ellen = 5,91m entspricht.
Dies geschieht allerdings nur dadurch, dass zwischen dem Kapitell und dem Gewölbe-kämpfer lt. Aufmassblatt Nr.53 eine Überhöhung von 75cm eingefügt wurde.
Ich vermute, dass die Raumproportionen für Grundrissmaße wegen der notwendigen präzisen Vorgaben für später einzufügende Gewölbe exakt nach der Regel „ad quadratum“ festgelegt wurden, im Aufriss aber nur ungefähr. Die Ausführung erfolgte dann in den handwerklich einfachen, bekannten Messmethoden mit einer Knotenleine in den Maßen Ellen oder Fuß.
Die exakte Festlegung der Mittelpunkte der Dienste nach den Regeln des „ad quadratum“ war also wichtig für die Konstruktionspunkte der Gewölbeauflager. Und die Gewölbe, wie wurden sie konstruiert? Das soll im Folgenden untersucht werden.
B. wie wurden die Gewölbe des Mittelschiffs konstruiert
Wie wurden die Gewölbe über den Diensten konstruiert? Die Mittelpunkte der Dienste waren mit 5,91m (10 Ellen) zu 8,358m (5,91 x √2) nach den Regeln des „ad quadratum“ festgelegt.
Die Form der Gewölbe war auch schon am Anfang der Planung festgelegt, denn mit der Herstellung der Gewölbeanfänger, die Teil des Mauerwerks sind, wurde bereits die Richtung, die Spannung (Bogen) und das Rippenprofil genau vorgegeben.
Mit dem Bau des Mittelschiffs wurde 1420 begonnen. Es war ein Sterngewölbe geplant für einen Raum bis ins Firmament! Ein Gewölbe, das erst ca. 100 Jahre später ab 1524 eingesetzt wurde,
Wie wurde dieses Sterngewölbe über dem Mittelschiff konstruiert und wie war es möglich die Informationen zur Konstruktion und Anfertigung der Gewölbe über Generationen unter den Stein-metzen weiterzugeben.
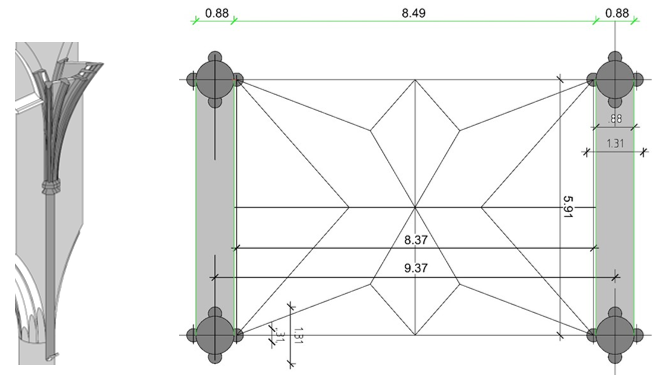
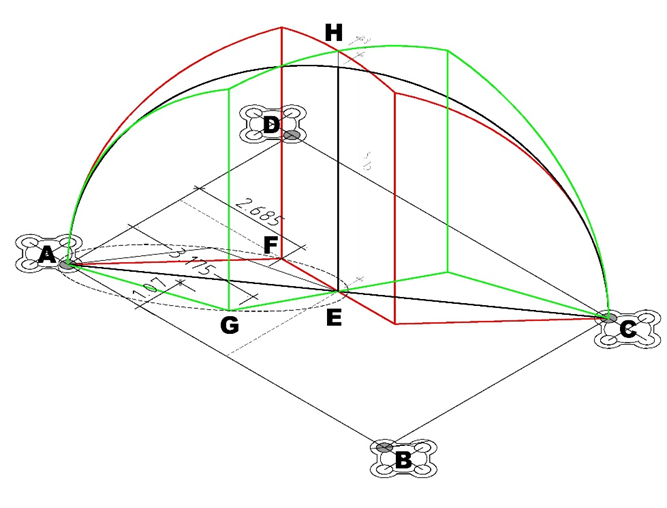
Hier links ein Gewölbeanfänger und rechts der Gewölbegrundriss eines Jochs im Mittelschiff des Münsters. Von den Diensten steigen aufgefächert und abgewinkelt Gewölberippen bis zum Gewölbescheitel auf. Wie wurde dieser Rippenstern konstruiert?
Das Gewölbe soll im Zentrum einen sechsteiligen Rippenstern bilden, der von acht paarweise aus den vier Diensten bzw. Kapitellen aufsteigenden Rippen getragen wird. Seitlich abstützende Rippen führen vom Rippenstern zum Scheitelpunkt der kräftigeren Gurtrippen, welche die Joche begrenzen.
Eigentlich besteht dieses Gewölbe nur aus zwei Rippen. Sowohl die roten wie die grünen Linien von A über E nach C ergeben gespiegelt die Rippenbögen von B über E nach D und bilden damit das gesamte Sterngewölbe.
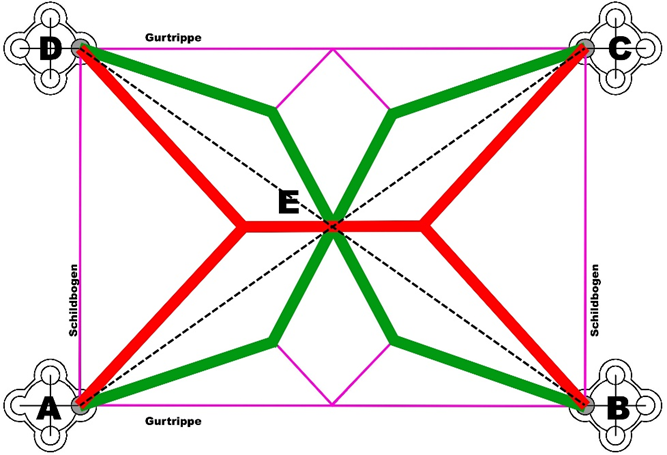
Durch das Aufmaßblatt Nr.53 ist die Form des Gewölbes genau rekonstruierbar. Nach welchen handwerklichen Regeln wurde aber ursprünglich die Geometrie der Rippenbögen ermittelt?
Die Gewölberippen sind aus vielen Steinen mit gleichem Querschnitt zusammengefügt. Bauökonomisch vorteilhaft ist, wenn ein Gewölbe aus Rippen möglichst gleicher Spannung (Rundung) zusammengesetzt ist.
hier das Aufmassblatt Nr 53 vom ersten Joch im Mittelschiff.
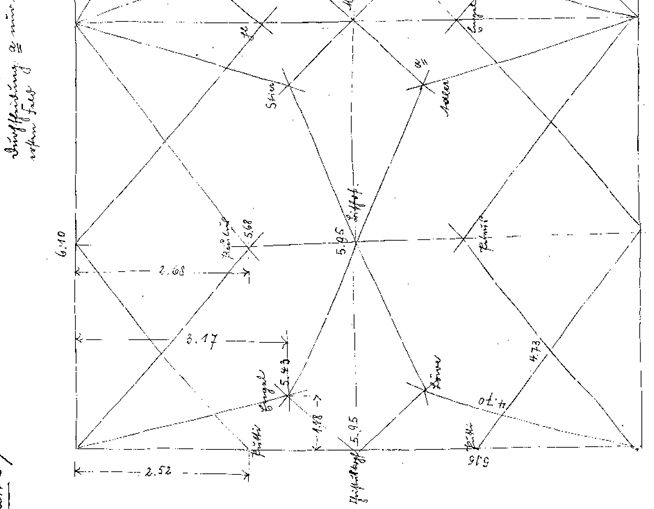
oben: der Grundriss des Gewölbejochs mit Massangaben
unten: Detailzeichnungen zu Gewölbeanfänger und Rippenprofilen
Bei einem Kreuzgewölbe wie im Chor des Münsters entspricht die Spannung (Spannweite) der diagonal laufenden Rippe dem Abstand der Dienst-Mittelpunkte.Die Rippe bildet einen Halbkreis, der Rippenscheitel entspricht dem Radius. (schwarze Linien)
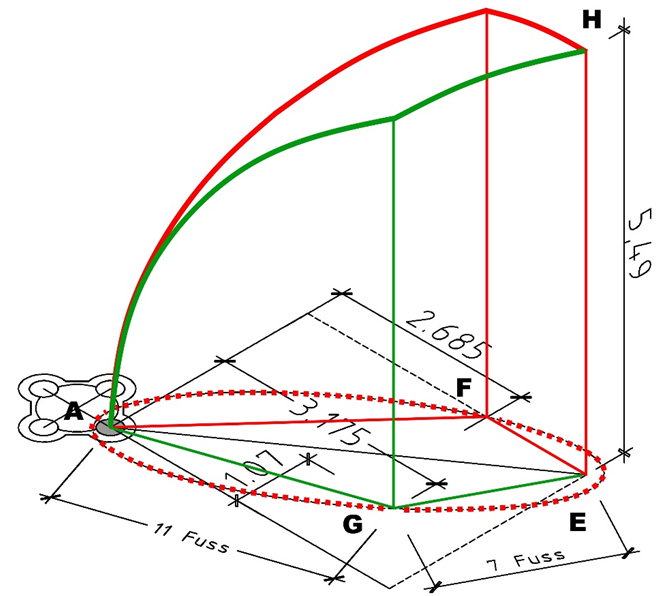
Bei einem Sterngewölbe wie im Mittelschiff des Münsters ist die Spannweite des Rippenbogens aber durch die Faltung des Rippenverlaufs größer als die Entfernung der Dienst-Mittelpunkte
(siehe Verlauf der roten bzw. grünen Linien). Aus dem Aufmaß ergab sich eine Spannweite von ca. 11 Meter.
Dies läßt vermuten, dass bei der Konstruktion auf dem Reiss-boden der Bauhütte mit einer Knotenleine (empirisch) ein Maß von 36 Fuss (36 x 0,3048 m = 10,9728 m) festgelegt wurde.
Im folgenden habe ich versucht, die ursprüngliche Konstruktionsweise nachzuvollziehen.
Wie zuvor beschrieben, war das Jochmaß des Mittelschiffs mit 4 Ellen zu 4 x√2 Ellen nach der Regel „ad quadratum“ festgelegt worden und für die Spannweite der Gewölberippen 36 Fuss.
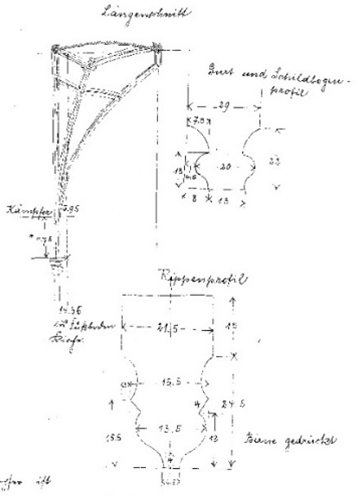
Der folgende Plan zeigt ¼ eines Gewölbejochs im Mittelschiff:
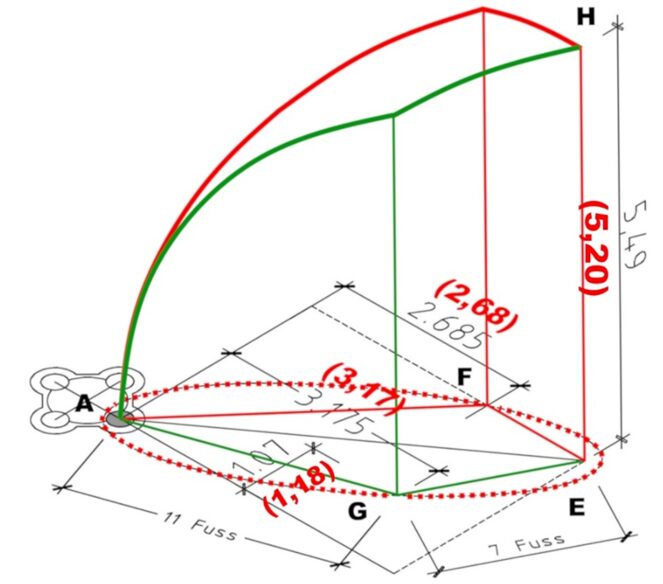
A = das Rippenauflager (der Kämpfer) eines Dienstes, E = die Jochmitte und H = der Gewölbescheitel
Auf dem Reissboden der Bauhütte aufgezeichnet, genügt dieser Teilgrundriss zur Berechnung des genauen Rippenverlaufs
Unter der Vorgabe, dass die Spannung aller Rippen, auch der Gurt- und Schildbogen-profile, gleich sein soll, muß auch die Länge der Strecken A-F-E und A-G-E gleich sein. Die Lage der Punkte F und G, an denen die Rippen ihre Richtung ändern und zum Scheitelpunkt H weiterlaufen, wurde ermittelt mit die Ellipsen-Formel.
Die Ellipsenformel besagt, dass die Summe der Entfernungen jedes Punktes auf einer Ellipse zu den beiden Brennpunkten immer gleich ist.
Die beiden Brennpunkte sind in unserer Zeichnung das Rippenauflager A und die Mitte des Gewölbejochs E. Die Länge der Strecke A-F-E und A-G-E, beträgt 18 Fuss, also 18 Knoten der als Messband üblichen Knotenleine.
Mit 2 Nägeln als Brennpunkte der Ellipse und einer dazwischen gespannten Leine von 18 Knoten Länge läst sich auf einfachste Weise die Ellipse auf den Reissboden der Bauhütte zeichnen. Der Schnittpunkt der Ellipse mit der Mittellinie des Jochs ergibt den Punkt F, an dem sich die Richtung des Rippenverlaufs (rot) ändert, quer zur Schiffsrichtung bis zum Gewölbemittelpunkt E.
Für die weitere Rippe (grün) sollte ein Verlauf gefunden werden, der die erste Rippe (rot) unter ca. 60 Grad schneidet. Dadurch entsteht in der Jochmitte ein fast gleichmäßiger 6-teiliger Rippen-stern. Hierfür spannte man die 18-teilige Knotenleine, in 11 und 7 Knoten / Fuss unterteilt, und legte so den Knickpunkt fest.
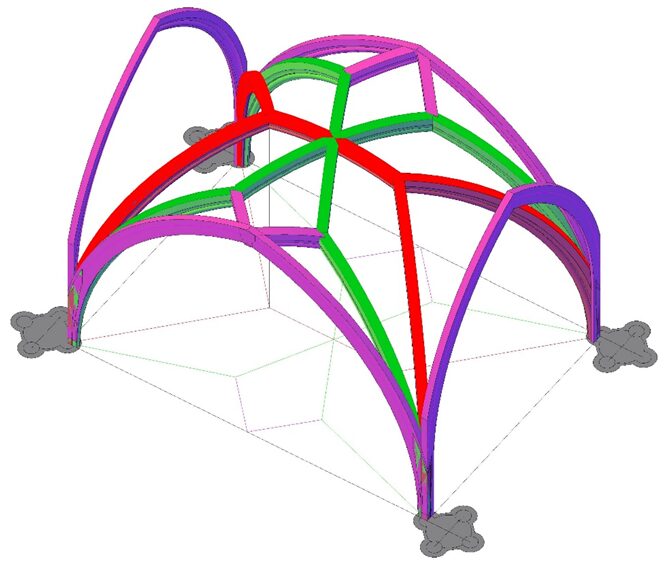
Die in dieser Zeichnung rot und grün dargestellten Rippen bilden mit den Bogensegmen-ten der Gurt- und Scheidbogenprofile (magenta) ebenfalls gleicher Spannung das gesamte Sternengewölbe. Es haben also alle Rippen die gleiche Spannweite von 36 Fuss = 10,98 m und das Gewölbe eine Scheitelhöhe von 18 Fuss = 5,49m.
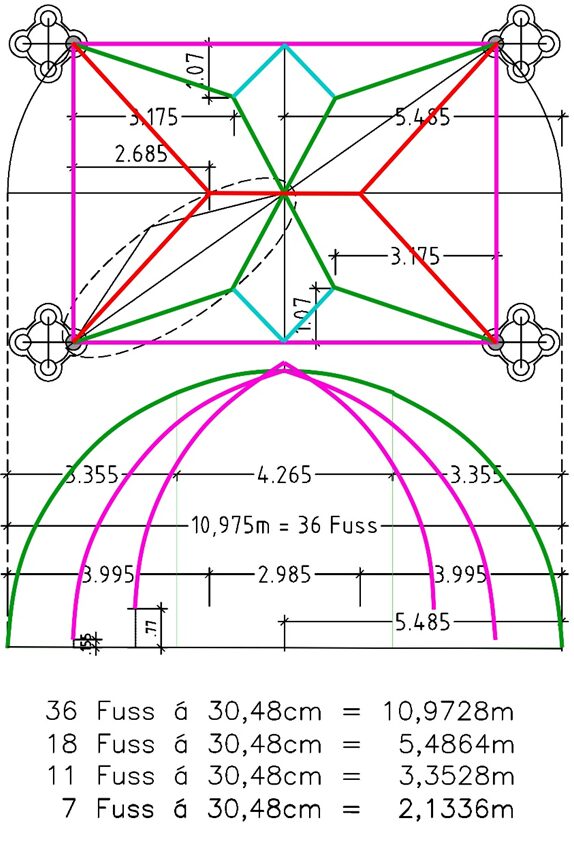
dieses Maßblatt (oben) zeigt die Radien aller Rippen und Rippensegmente gleicher Größe mit r = 5,485m oder 18 Fuß
In der folgenden Konstruktionszeichnung sind die aufgemessenen (rot) und die errechneten Maße eingezeichnet. Sie stimmen fast vollständig überein.
Nur der Abstand zur Quergurtachse weicht ab und ist errechnet mit 1,07m, im Aufmass ist 1,18m eingetragen. Dieses Maß wurde im 1. Joch gemessen und bezieht sich vermutlich auf den Abstand zum Triumphbogen.
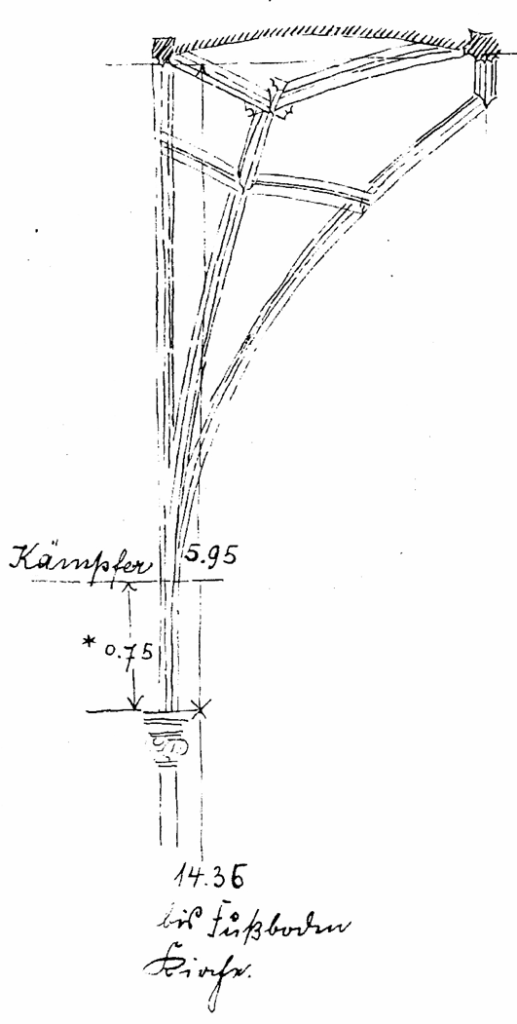
Das folgende Aufmaß zeigt, dass zwischen Kapitell und Kämpfer eine Überhöhung von 75 cm eingefügt wurde, sodass der Gewölbescheitel auf 5,95m über Kapitell und 20,30m über Fußboden ansteigt. Die Raumwirkung des Mittelschiffs wurde dadurch nochmals gesteigert. Im Querschnitt entspricht jetzt die gesamte Raumproportion fast genau den Regeln des „ad quadratum“ mit zwei Joch-Längen (2x 5,91m) plus einer Joch-Breite (5,91m x √2) = 20,18m Raumhöhe.
Mit der Regel „ad quadratum“ und mit der Kenntnis weniger mathematisch-geometrischer Gesetze waren die Sternengewölbe im Mittelschiff des Überlinger Münsters sehr einfach zu konstruieren und die Konstruktionsweise auch viele Generationen später für eine Fertigstellung der Gewölbe exakt nachzuvollziehen (Gewölbeanfänger ca.1420, Gewölbe-einbau erst ab 1524)
Es genügten dazu nur die folgenden Angaben:
- eine Skizze des geplanten 6-teiligen Rippensterns
- das Jochmaß mit 10 Ellen für die Gewölbegröße
- die Rippenspannung mit 36 Fuß oder den Gewölbescheitel von 18 Fuß über Kämpfer
- eine Schablone des geplanten Rippenquerschnitts
C. verschiedene Maßwerkkonstruktionen der Fenster am Überlinger Münster
Im Folgenden möchte ich die Regel „ad triangulum“ am Maßwerk dieser drei unterschiedlichen Fenster des Überlinger Münsters untersuchen.

- das mittlere Chorfenster, ab ca. 1350

2. das mittlere Giebelfenster, ab ca. 1420

3. das Obergadenfenster, ab ca. 1425
Diese Zeichnung zeigt die drei unterschiedlichen Konstruktionsweisen der obigen Münsterfenster
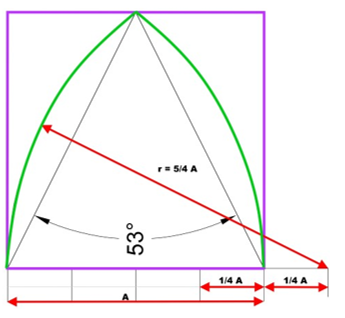
1. die schmale Form: ein gleichschenkliges Dreieck im Quadrat
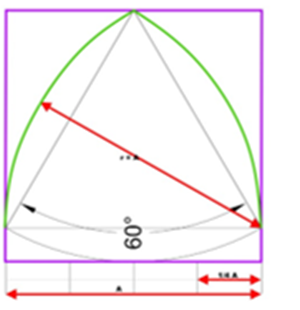
2. die mittlere Form: ein gleichseitiges Dreieck im Quadrat
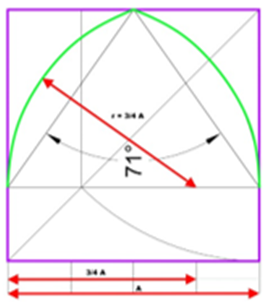
3. die breite Form: ein gleichschenkliges Dreieck im Rechteck, unterteilt nach der Regel „ad quadratum“
- das Maßwerk des mittleren Chorfensters

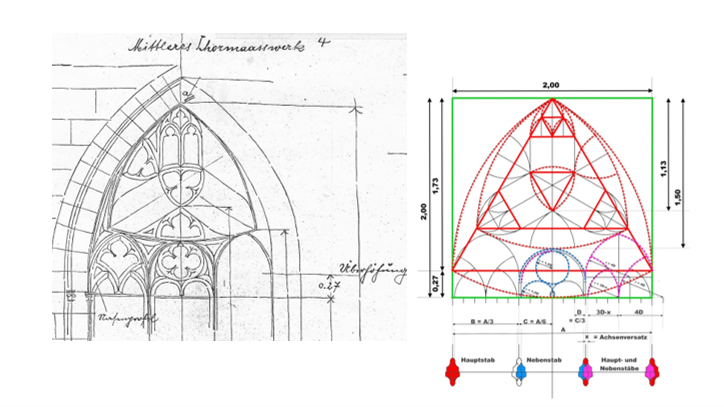
Aus der Aufmaß-Zeichnung Blatt Nr.28 ergibt sich, dass die äußeren Konstruktionslinien des gesamten Maßwerks (ohne Leibung) ein Quadrat bilden.
In dieses Quadrat ist eingeschlossen ein gleichseitiges Dreieck, über dessen Seitenlinien ein Bogen mit dem Radius der Seitenlänge des Quadrats den oberen Teil des gotischen Maßwerks über dem Kämpfer bildet
die einzelnen Konstruktionsschritte für das Maßwerk sind hier dargestellt
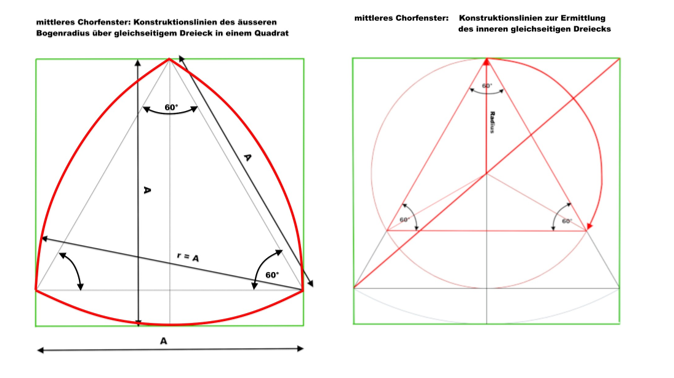
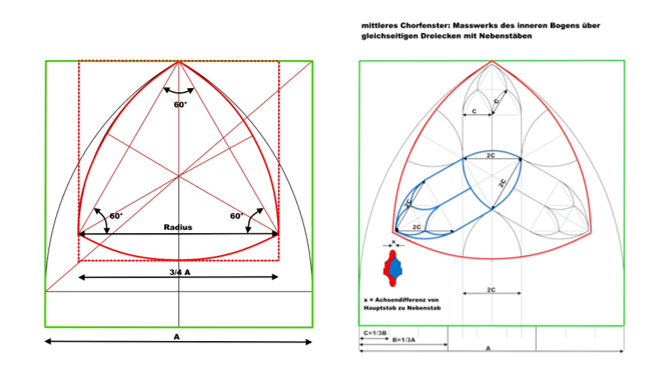
der obere Teil des Maßwerks ist nur aus Kreissegmenten über gleichseitigen Dreiecken gebildet, der untere Teil aus Segmenten mit verschiedenen Radien, die sich aus Zwei- oder Dreiteilungen der Fensterbreite ergeben
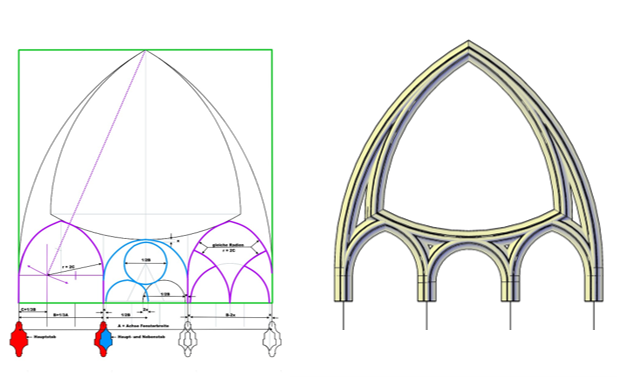
2. das Maßwerk des mittleren Giebelfensters

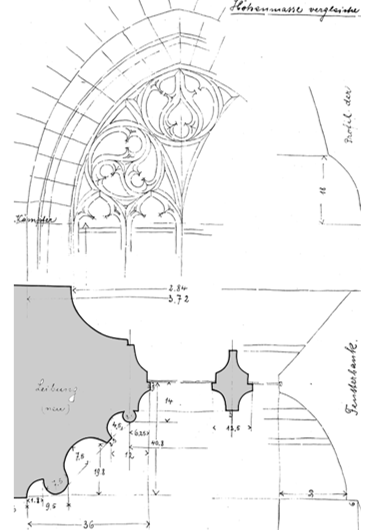
dieses Aufmaßblatt Nr. 49 zeigt ein gotisches vierteiliges Fenster, durch Pfosten gegliedert und mit einem seitlichen Gewände, das in der Tiefe mit Wulsten und Kehlen gestaffelt ist.
den Fensterabschluss bildet ein Maßwerk aus Bögen, Kreisen, Fischblasen und Nasen
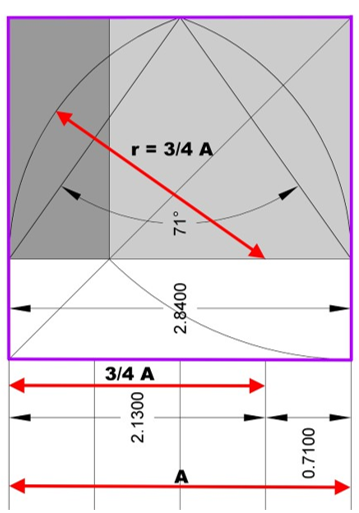
Dieses Maßwerk ist nicht über einem Quadrat oder gleichseitigen Dreieck entworfen, sondern über einem nach den Regeln des „ad quadratum“ gebildeten Rechteck.
Der Radius der Kreissegmente beträgt 3/4 der Gesamtbreite
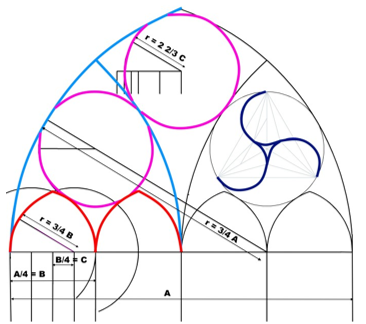
Je 2 Fensterfelder sind durch symmetrische Bogensegmente zusammengefasst, die in ihrer Spannung den äußeren Bögen des Maßwerks entsprechen
Jedes einzelne Fensterfeld ist nach dem gleichen Konstruktionsprinzip durch Bogensegmente mit r=3/4 Fensterbreite geschlossen.
hier das Giebelfenster in zwei dreidimensionalen CAD-Zeichnungen
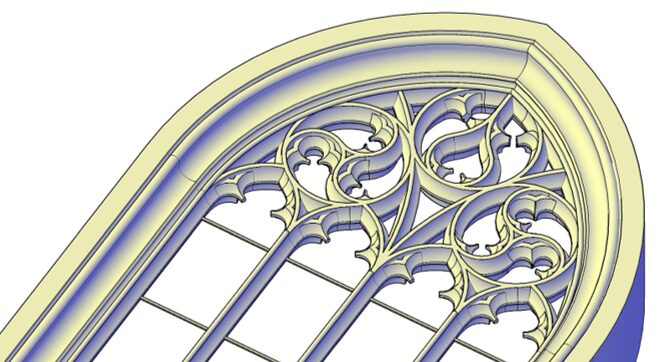

3. das Maßwerk des Obergadenfensters

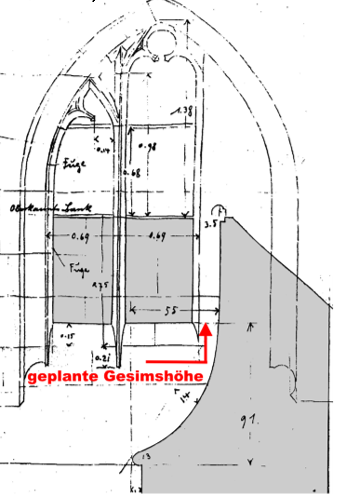
hier ein Ausschnitt aus dem Aufmassblatt 59 zum Fenster im Obergaden,
Bei Einstellung des Baus der Hallenkirche ca. 1424 und der Umplanung und Einfügung eines Obergadens sollten die Fenster sehr viel Licht in das Innere des Mittelschiffs bringen. Dazu mussten sie einen möglichst breiten Fensterbogen erhalten.
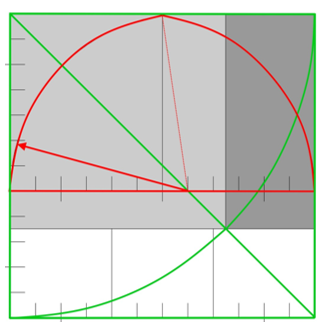
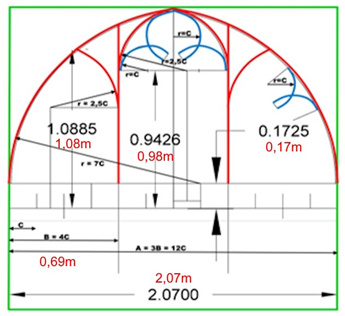
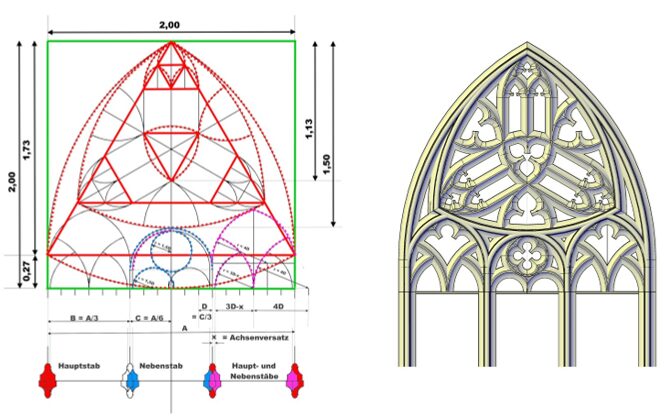
Die obere Zeichnung zeigt das Maßwerk des Obergadens, ein-gebunden in ein Quadrat, die Seiten in 24 Teile untergliedert.
Das graue Rechteck in diesem Quadrat hat ein Seitenverhältnis von 24 zu 17 = 1,4117 (nach der Regel „ad quadratum“ 1,4142)
In dem Rechteck bildet die Fläche oberhalb des Kämpfers ein Maßwerk mit 14 Teilen Höhe und 24 Teilen Breite, die untere Fläche eine Überhöhung von 3 Teilen. Der Radius der großen Bogensegmente beträgt 14 Teile, die Radien der kleineren 5 Teile und die der Nasen 2 Teile.
In der unteren Zeichnung sind sowohl die Werte gem. Aufmaß (rot) wie die errechneten Werte eingetragen.
Die Gesamtbreite wird aufgeteilt in 3 Fensterbahnen und diese wiederum 4-fach geteilt. Jedes Einzelteil, hier mit C bezeichnet, beträgt also 1/12 der Gesamtbreite. Dieses Maß C bildet das Grundmaß der Bogenradien im Fenstermaßwerk: der Radius des großen äußeren Bogens beträgt 7 x C, die kleineren Bögen 2,5 x C und für die „Nasen“ beträgt der Radius 1 x C. Die „Nasen“ ergeben sich durch die Überschneidung der Radien bzw. der Profile.
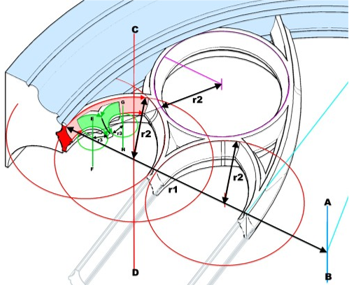
hier in 3D-Zeichnung die schrittweise Darstellung einzelner Konstruktionsdetails am Beispiel des mittleren Giebelfensters
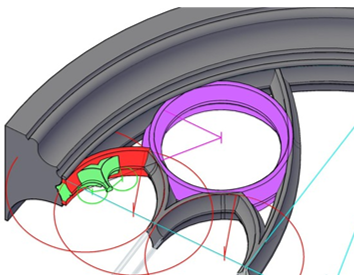
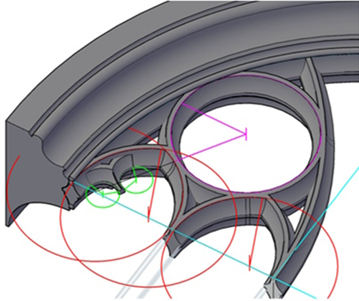
eine Idee, eine räumliche Vorstellungskraft, der Wagemut statischer Konstruktionen, die grundlegenden Kenntnisse geometrischer Gesetze, ein grafisches Darstellungsvermögen, große handwerkliche Steinmetzkunst, so entstanden mit unermüdlichem Fleiß großartige Bauwerke
das Ergebnis meiner Untersuchungen:
In der ersten gotischen Bauphase ab 1350 wurde für den neuen Chor die Raumbreite der romanischen Basilika übernommen Weder im Grund- noch Aufriss des Chores ist die Regel „ad quadratum“ erkennbar.
Ganz sicher aber wurde sie angewendet beim zweiten gotischen Bauabschnitt. Auf ihr basiert der Entwurf der geplanten großen Hallenkirche um 1420 und auch die Planänderung um ca. 1425 mit niedrigeren Seitenschiffen.
Nach Aufgabe auch dieser Planungsphase, dem Abbruch der romanischen Basilika 1429 und dem Weiterbau zu einer fünf-schiffigen Basilika mit abgestuften, niedrigen Seitenschiffen ist die Anwendung der Regel „ad quadratum“ nicht mehr erkennbar.
Diese Änderung hatte außerdem zur Folge, dass die geplanten hohen gotischen Fensterformen an der Süd- und Nordfassade nicht mehr möglich waren und die bereits vorhandenen Fenster-Gewände mit einem flachen Tudorbogen abgeschlossen werden mussten.
Die Regeln „ad quadratum“ und „ad triangulum“ lassen sich aber in unterschiedlichen Spielformen an den Fenstern des Chores, des Westgiebels und des Obergadens nachvollziehen.
Am Anfang meiner Studien stand ein interessantes Kapitel über
…geometrische Regeln, die von den Baumeistern der großen gotischen Kathedralen angewendet wurden…
Das Ergebnis dieser Studien zeigt:
in den entscheidenden Phasen zwischen 1420 und 1429 wurde das Überlinger Münster nach den gleichen Regeln wie die großen gotischen Kathedralen geplant und gebaut.
Carl Fahr, Dipl. Ing. Architekt BDA
Juli 2025
Schreibe einen Kommentar